Camino más corto (teoria de grafos) investigación de operaciones
Los problemas conocidos como problemas del camino mínimo o camino más corto, tratan como su nombre indica de hallar la ruta mínima o más corta entre dos puntos. Este mínimo puede ser la distancia entre los puntos origen y destino o bien el tiempo transcurrido para trasladarse desde un punto a otro. Se aplica mucho para problemas de redes de comunicaciones.
Este tipo de problemas pueden ser resueltos por el método del Simplex, sin embargo existen otros métodos más eficientes como por ejemplo el algoritmo de Dijkstra o el de Bellman-Ford.
Este algoritmo calcula el camino mínimo de un nodo a a otro nodo z en particular, a la vez que calcula los caminos mínimos desde el nodo inicial a dado hasta cada uno de los otros nodos del grafo.
Consiste en encontrar la ruta más corta entre dos nodos dados de un grafo dirigido y valuado (con capacidades). Veremos dos algoritmos, por un lado el algoritmo de Dijkstra, que encuentra el camino más corto entre el nodo origen y cada uno de los otros nodos de la red, y por otro lado el algoritmo de Floyd, que encuentra el camino más corto entre cualquier par de nodos de la red.
Algoritmo de DIJKSTRA
Tendremos a lo largo de todo el proceso dos conjuntos y dos vectores:
- Conjunto C : Conjunto de vértices candidatos. Inicialmente contiene todos los nodos menos el nodo origen.
- Conjunto S : Conjunto de vértices seleccionados, es decir, aquellos para los que ya conocemos su camino mínimo desde el nodo origen. Inicialmente contiene el nodo origen.
- Vector D : Almacenará la longitud del camino más corto desde el origen a cada nodo. Tendrá tantas posiciones como nodos tenga el grafo. El coste de ir del nodo origen a sí mismo lo estimaremos como cero.
- Vector P : Almacenará el nodo predecesor a cada nodo en el camino más corto desde el origen hasta él. Tendrá tantas posiciones como nodos tenga el grafo. La posición del nodo predecesor al origen estableceremos que sea cero para indicar que es el nodo origen.
- Llamaremos al nodo origen o, y el coste de ir del nodo i al nodo j lo denotaremos como COSTEij .
Hay que seguir los siguientes pasos:
- Seleccionamos el nodo que sea destino de la arista con menor valor que salga del nodo o, llamémoslo u. Introducimos el nodo u en S y lo sacamos de C. Almacenamos en la posición u del vector D el valor COSTEou y en la posición u del vector P el valor del nodo predecesor, es decir, o.
- Seleccionamos el siguiente nodo al que podamos llegar con menor coste, bien directamente desde o, bien a través del otro nodo seleccionado u. Llamamos al nuevo nodo seleccionado v. Introducimos el nodo v en S y lo sacamos de C. Introducimos en la posición v del vector D el coste de llegar al nodo v, si es directamente desde o será COSTEov, si es a través de u será D[u]+COSTEuv. Por último, en la posición v del vector P introducimos el valor del nodo predecesor, ya sea o o u.
- Repetiremos este proceso hasta que todos los nodos hayan sido seleccionados, es decir, hasta que el conjunto C esté vacío, o lo que es lo mismo, hasta que en el conjunto S se encuentren todos los nodos del grafo. En ese momento en el vector D tendremos almacenado el coste mínimo para llegar desde el nodo origen a cualquier nodo del grafo, y podremos obtener el camino más corto mediante el vector P.
Ejemplo: Aplicar el algoritmo de Dijkstra sobre el siguiente grafo siendo el nodo origen el 1:
Algoritmo DE FLOYD
El algoritmo de Floyd es más general que el de Dijkstra, ya que determina la ruta más corta entre dos nodos cualquiera de la red.
- El algoritmo representa una red de n nodos como una matriz cuadrada de orden n, la llamaremos matriz C. De esta forma, el valor Cijrepresenta el coste de ir desde el nodo i al nodo j, inicialmente en caso de no existir un arco entre ambos, el valor Cij será infinito.
- Definiremos otra matriz D, también cuadrada de orden n, cuyos elementos van a ser los nodos predecesores en el camino hacia el nodo origen, es decir, el valor Dij representará el nodo predecesor a j en el camino mínimo desde i hasta j. Inicialmente se comienza con caminos de longitud 1, por lo que Dij = i.
- Las diagonales de ambas matrices representan el coste y el nodo predecesor para ir de un nodo a si mismo, por lo que no sirven para nada, estarán bloqueadas.
Los pasos a dar en la aplicación del algoritmo de Floyd son los siguientes:
- Formar las matrices iniciales C y D.
- Se toma k=1.
- Se selecciona la fila y la columna k de la matriz C y entonces, para i y j, con i≠k, j≠k e i≠j, hacemos:
Si (Cik + Ckj) < Cij → Dij = Dkj y Cij = Cik + Ckj
En caso contrario, dejamos las matrices como están.
- Si k ≤ n, aumentamos k en una unidad y repetimos el paso anterior, en caso contrario paramos las iteraciones.
- La matriz final C contiene los costes óptimos para ir de un vértice a otro, mientras que la matriz D contiene los penúltimos vértices de los caminos óptimos que unen dos vértices, lo cual permite reconstruir cualquier camino óptimo para ir de un vértice a otro.
Ejemplo: Aplicar el algoritmo de Floyd sobre el siguiente grafo para obtener las rutas más cortas entre cada dos nodos. El arco (3, 5) es direccional, de manera que no está permitido ningún tráfico del nodo 5 al nodo 3 . Todos los demás arcos permiten el tráfico en ambas direcciones.
Tomamos i=2 (i ≠k):
- j=3 (j≠k, j≠i): C[2,1]+C[1,3] = 3+10 = 13 < C[2,3] = ∞, por tanto hacemos:
C[2,3] = 13 y D[2,3] = 1.
- j=4 (j≠k, j≠i): C[2,1]+C[1,4] = 3+∞ = ∞, no hay que cambiar nada, no podemos llegar de 2 a 4 a través de 1.
- j=5 (j≠k, j≠i): C[2,1]+C[1,5] = 3+∞ = ∞, no hay que cambiar nada, no podemos llegar de 2 a 5 a través de 1.
- Tomamos i=3 (i ≠k):
- j=2 (j≠k, j≠i): C[3,1]+C[1,2] = 10+3 = 13 < C[3,2] = ∞, por tanto hacemos:
C[3,2] = 13 y D[3,2] = 1.
- j=4 (j≠k, j≠i): C[3,1]+C[1,4] = 10+∞ = ∞, no hay que cambiar nada, no podemos llegar de 3 a 4 a través de 1.
- j=5 (j≠k, j≠i): C[3,1]+C[1,5] = 10+∞ = ∞, no hay que cambiar nada, no podemos llegar de 3 a 5 a través de 1.
- Tomamos i=4 (i ≠k):
- j=2 (j≠k, j≠i): C[4,1]+C[1,2] = ∞+3 = ∞, no hay que cambiar nada, no podemos llegar de 4 a 2 a través de 1.
- j=3 (j≠k, j≠i): C[4,1]+C[1,3] = ∞+10 = ∞, no hay que cambiar nada, no podemos llegar de 4 a 3 a través de 1.
- j=5 (j≠k, j≠i): C[4,1]+C[1,5] = ∞+∞ = ∞, no hay que cambiar nada, no podemos llegar de 4 a 5 a través de 1.
Tomamos i=5 (i ≠k), en este caso ocurre como en el paso anterior, como C[5,1]=∞, entonces no habrá ningún cambio, no puede haber ningún camino desde 5 a través de 1.
Tomamos k=2:

Tomamos i=1:
- j=3: C[1,2]+C[2,3] = 3+13 = 16 > C[1,3] = 10 , por tanto no hay que cambiar nada, el camino es mayor que el existente.
- j=4: C[1,2]+C[2,4] = 3+5 = 8 < C[1,4] = ∞, por tanto hacemos:
C[1,4] = 8 y D[1,4] = 2 .
- j=5: C[1,2]+C[2,5] = 3+∞ = ∞, no hay que cambiar nada.
- Tomamos i=3:
- j=1: C[3,2]+C[2,1] = 13+3 = 16 > C[3,1] = 10, no hay que cambiar nada.
- j=4: C[3,2]+C[2,4] = 13+5 = 18 > C[3,4] = 6, no hay que cambiar nada.
- j=5: C[3,2]+C[2,5] = 13+∞ = ∞, no hay que cambiar nada.
- Tomamos i=4:
- j=1: C[4,2]+C[2,1] = 5+3 = 8 < C[4,1] = ∞, por tanto hacemos:
C[4,1] = 8 y D[4,1] = 2.
- j=3: C[4,2]+C[2,3] = 5+13 = 18 > C[4,3] = 6, no hay que cambiar nada.
- j=5: C[4,2]+C[2,5] = 5+∞ = ∞, no hay que cambiar nada.
Tomamos i=5, como C[5,2]=∞, entonces no habrá ningún cambio.
- Tomamos i=1:
- j=2: C[1,3]+C[3,2] = 10+13 = 23 > C[1,2] = 3, no hay que cambiar nada.
- j=4: C[1,3]+C[3,4] = 10+6 = 16 > C[1,4] = 8, no hay que cambiar nada.
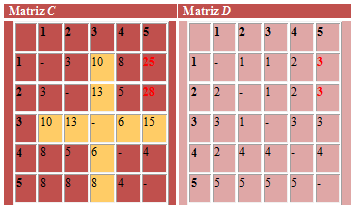
- j=5: C[1,3]+C[3,5] = 10+15 = 25 < C[1,5] = ∞, por tanto hacemos:
C[1,5] = 25 y D[1,5] = 3 .
- Tomamos i=2:
- j=1: C[2,3]+C[3,1] = 13+10 = 23 > C[2,1] = 3, no hay que cambiar nada.
- j=4: C[2,3]+C[3,4] = 13+6 = 19 > C[2,4] = 5, no hay que cambiar nada.
- j=5: C[2,3]+C[3,5] = 13+15 = 28 < C[2,5] = ∞, por tanto hacemos:
C[2,5] = 28 y D[2,5] = 3.
- Tomamos i=4:
- j=1: C[4,3]+C[3,1] = 6+10 = 16 > C[4,1] = 8, no hay que cambiar nada.
- j=2: C[4,3]+C[3,2] = 6+13 = 19 > C[4,2] = 5, no hay que cambiar nada.
- j=5: C[4,3]+C[3,5] = 6+15 = 21 > C[4,5] = 4, no hay que cambiar nada.
Tomamos i=5, como C[5,3]=∞, entonces no habrá ningún cambio.
Tomamos k=4:

- Tomamos i=1:
- j=2: C[1,4]+C[4,2] = 8+5 = 13 > C[1,2] = 3, no hay que cambiar nada.
- j=3: C[1,4]+C[4,3] = 8+6 = 14 > C[1,3] = 10, no hay que cambiar nada.
- j=5: C[1,4]+C[4,5] = 8+4 = 12 < C[1,5] = 25, por tanto hacemos:
C[1,5] = 12 y D[1,5] = 4.
- Tomamos i=2:
- j=1: C[2,4]+C[4,1] = 5+8 = 13 > C[2,1] = 3, no hay que cambiar nada.
- j=3: C[2,4]+C[4,3] = 5+6 = 11 < C[2,3] = 13, por tanto hacemos:
C[2,3] = 11 y D[2,3] = 4.
- j=5: C[2,4]+C[4,5] = 5+4 = 9 < C[2,5] = 28, por tanto hacemos:
C[2,5] = 9 y D[2,5] = 4.
- Tomamos i=3:
- j=1: C[3,4]+C[4,1] = 6+8 = 14 > C[3,1] = 10, no hay que cambiar nada.
- j=2: C[3,4]+C[4,2] = 6+5 = 11 < C[3,2] = 13, por tanto hacemos:
C[3,2] = 11 y D[3,2] = 4.
- j=5: C[3,4]+C[4,5] = 6+4 = 10 < C[3,5] = 15, por tanto hacemos:
C[3,5] = 10 y D[3,5] = 4.
- Tomamos i=5:
- j=1: C[5,4]+C[4,1] = 4+8 = 12 < C[5,1] = ∞, por tanto hacemos:
C[5,1] = 12 y D[5,1] = 2 .
- j=2: C[5,4]+C[4,2] = 4+5 = 9 < C[5,2] = ∞, por tanto hacemos:
C[5,2] = 9 y D[5,2] = 4.
- j=3: C[5,4]+C[4,3] = 4+6 = 10 < C[5,3] = ∞, por tanto hacemos:
C[5,3] = 10 y D[5,3] = 4.
|
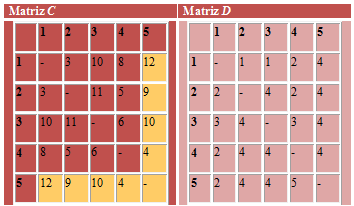
- Las matrices finales C y D contienen toda la información necesaria para determinar la ruta más corta entre dos nodos cualquiera de la red. Por ejemplo, la distancia más corta del nodo 1 al nodo 5 es C[1,5] = 12.
- Para determinar la ruta asociada del camino mínimo entre el nodo 1 y el nodo 5 haremos lo siguiente:
- Consultamos D[1,5]=4, por tanto el nodo predecesor al 5 es el 4, es decir, 4 → 5.
- Consultamos D[1,4]=2, por tanto el nodo predecesor al 4 es el 2, es decir, 2 → 4 → 5.
Consultamos D[1,2]=1, por tanto el nodo predecesor al 2 es el 1, es decir, 1 → 2 → 4 → 5, y así ya tenemos la ruta completa.
.







Comentarios
Publicar un comentario